Quadratic MSE Approximation 

 
This analysis requires us to build a quadratic approximation of the loss we would expect using weight w w.r.t optimal weight w*. 
 
I tried my best to reason the variables as it was not explained in the book so I would not be surprised if it's wrong. I am especially unconfident with the reasoning behind the Hessian and the 1/2 
 

Add Weight Regularization 

 
After the previous step of finding the derivative w.r.t to w, we add the weight regularization and find out that the eigenvectors of the Hessian has been scaled. 
 

Visualization 

 
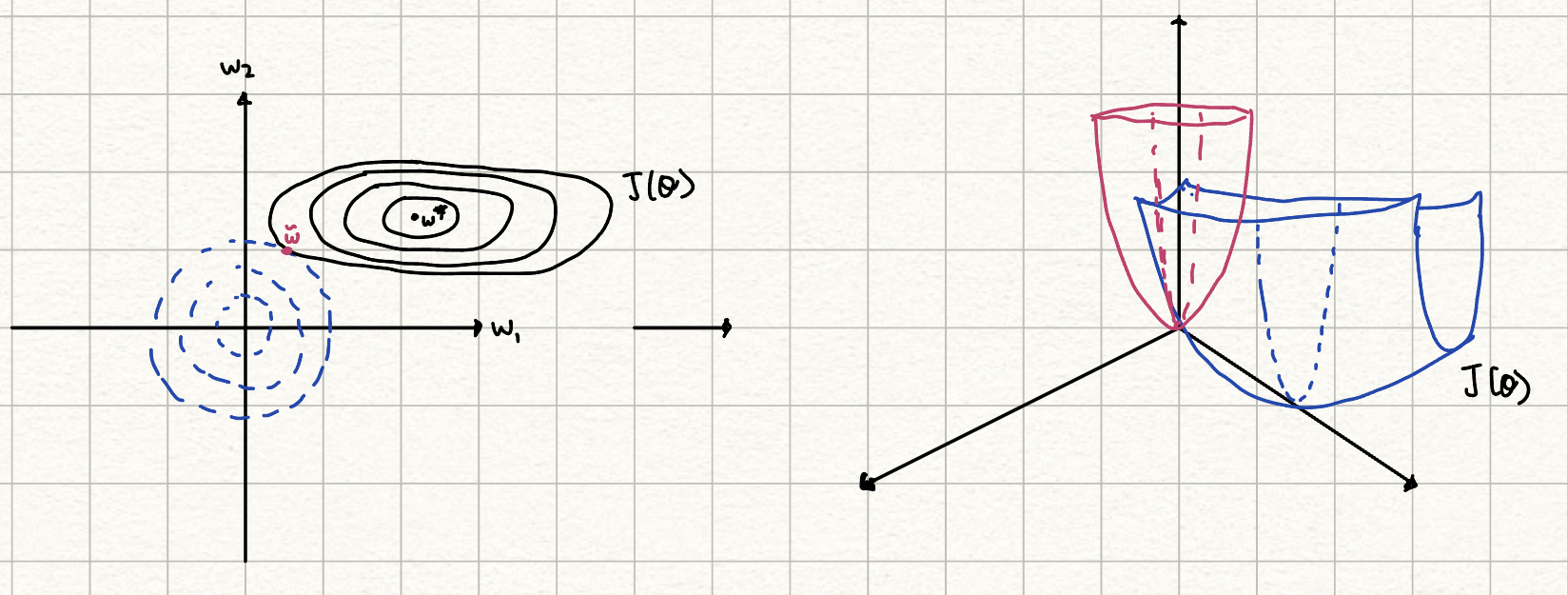
According to our previous analysis, the "weaker" eigenvalue gets scaled down, meaning that the regularization prioritizes more important eigenvectors. So from our contour graph, we see that w1 gets pulled closer to 0 whereas w2 does not get change a lot from its original value. 
 

Undetermined Problem 

 
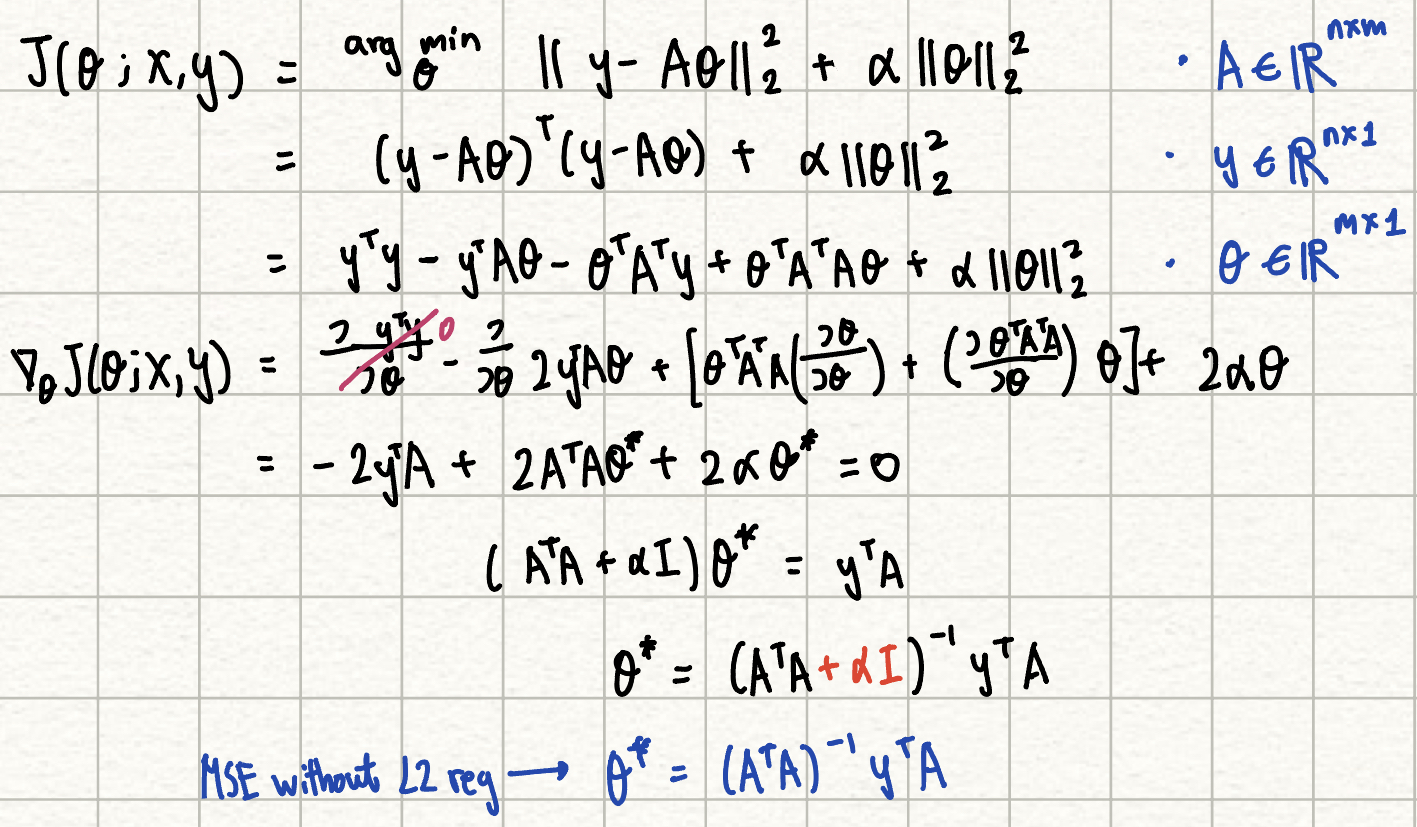
L2 regularization helps with underdetermined problems where the covariance matrix is non-invertible, which is crucial for closed-form solutions for PCA or linear regression. Hence with the additional alpha term L2 reg can turn the matrix into an invertible matrix.